The Triangle and Its Properties
Exercise 6.5
1). PQR is a triangle, right-angled at P. If PQ = 10cm and PR = 24 cm, find QR.
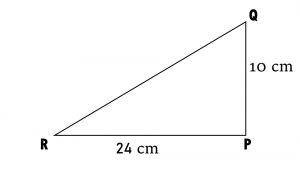
In DPQR, By Pythagorean Property
QR2 = PQ2 + PR2
QR2 = 102 + 242
QR2 = 100 + 576
QR2 = 676
Taking square root on both sides
√QR2 = √676
QR = 26 cm
2). ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
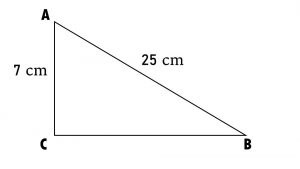
In DABC, By Pythagorean Property
AB2 = AC2 + BC2
252 = 72 + BC2
625 = 49 + BC2
625 – 49 = BC2
BC2 = 625 – 49
BC2 = 576
Taking square root on both sides
√BC2 = √576
BC = 24 cm
3). A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
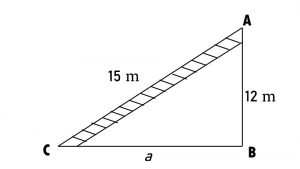
Let AB be the height of the window from the ground
BC be the distance of the ladder from the wall
AC be the length of the ladder
AC = 15 m
AB = 12 m
BC = ?
In DABC, By Pythagorean Property
AC2 = AB2 + BC2
152 = 122 + BC2
225 = 144 + BC2
225 – 144 = BC2
BC2 = 225 – 144
BC2 = 81
Taking square root on both sides
√BC2 = √81
BC = 9 m
Ans: the distance of the foot of the ladder from the wall is 9 m.
4). Which of the following can be the sides of a right triangle?
(i) 2.5 cm,6.5 cm, 6 cm
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm,6.5 cm, 6 cm
Greater side = 6.5 cm
6.52 = 42.25
62 = 36
2.52 = 6.25
62 + 2.52 = 36 + 6.25 = 42.25
62 + 2.52 = 6.52
By Pythagorean Property
Given triangle is right angled triangle.
(ii) 2 cm, 2 cm, 5 cm.
Greater side = 5 cm
52 = 25
22 = 4
22 = 4
22 + 22 = 4 + 4 = 8
22 + 22 ≠ 52
By Pythagorean Property
Given triangle is not a right angled triangle.
(iii) 1.5 cm, 2cm, 2.5 cm.
Greater side = 2.5 cm
2.52 = 6.25
22 = 4
1.52 = 2.25
22 + 1.52 = 4 + 2.25 = 6.25
22 + 1.52 = 2.52
By Pythagorean Property
Given triangle is right angled triangle.
5). A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

Let AC be the original height of the tree and the tree is broken at B touching the ground at D
AC = ?
AB = 5 m
AD = 12 m
In DABD, By Pythagorean Property
BD2 = AB2 + AD2
BD2 = 52 + 122
BD2 = 25 + 144
BD2 = 169
Taking square root on both sides
√BD2 = √169
BD = 13 m
But BC = BD
BC = 13 m
AC = 5 + BC
AC = 5 + 13
AC = 18 m
Ans: the original height of the tree is 18 m.
6). Angles Q and R of a DPQR are 25º and 65º.
Write which of the following is true:
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2

Solution:
by angle sum property of a triangle
mÐP + mÐQ + mÐR = 1800
mÐP + 250 + 650 = 1800
mÐP + 900 = 1800
mÐP = 1800 – 900
mÐP = 900
DPQR is a right angles triangle and QR is a hypotenuse
(i) PQ2 + QR2 = RP2
False
(ii) PQ2 + RP2 = QR2
True
(iii) RP2 + QR2 = PQ2
False
7). Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
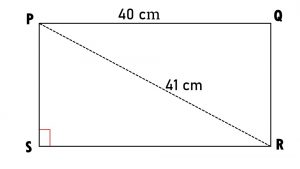
Let □PQRS is the given rectangle
Each angle of a rectangle is 900.
DPQR is a right angled triangle
In DPQR, By Pythagorean Property
PR2 = PQ2 + QR2
412 = 402 + QR2
1681 = 1600 + QR2
1681 – 1600 = QR2
QR2 = 1681 – 1600
QR2 = 81
Taking square root on both sides
√ QR2 = √81
QR = 9 cm
Length = 40 cm
Breadth = 9 cm
Perimeter= 2(L+B)
= 2(40+9)
= 2(49)
= 98 cm
Ans: Perimeter of the given rectangle = 98 cm
8). The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
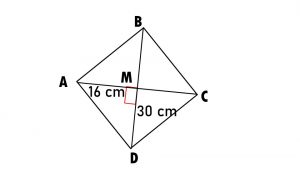
Let □ABCD is a rhombus
Diagonals AC and BD intersect each other at M
AC = 16 cm
BD = 30 cm
Diagonals of rhombus bisect each other at right angles
AM = ½ AC = ½ x 16 = 8 cm
DM = ½ BD = ½ x 30 = 15 cm
DAMD is a right angled triangle
By Pythagorean Property
AD2 = AM2 + DM2
AD2 = 82 + 152
AD2 = 64 + 225
AD2 = 289
Taking square root on both sides
√ AD2 = √289
AD= 17 cm
All the sides of rhombus are equal
Perimeter = 4 X side
= 4 X 17
= 68 cm
Click here for the solutions of
![]()