Lines and Angles

Exercise 5.2

1). State the property that is used in each of the following statements?

(i) If a || b, then ∠1 = ∠5.

(ii) If ∠4 = ∠6, then a || b.

(iii) If ∠4 + ∠5 = 180°, then a || b.

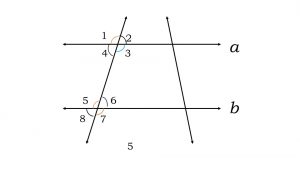
Answer:

(i) If a || b, then ∠1 = ∠5.

Corresponding angles property.

(ii) If ∠4 = ∠6, then a || b.

 The converse of alternate angles property.

(iii) If ∠4 + ∠5 = 180°, then a || b.

 Interior angles property.

2). In the adjoining figure, identify

(i) the pairs of corresponding angles.

(ii) the pairs of alternate interior angles.

(iii) the pairs of interior angles on the same side of the transversal.

(iv) the vertically opposite angles.

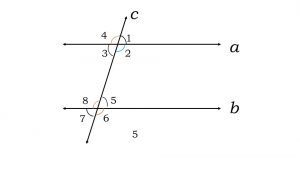
Answer:

(i) the pairs of corresponding angles.

  ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7 and ∠4 and ∠8

(ii) the pairs of alternate interior angles.

      ∠4 and ∠6 and ∠3 and ∠5

(iii) the pairs of interior angles on the same side of the transversal.

      ∠3 and ∠6 and ∠4 and ∠5

(iv) the vertically opposite angles.

      ∠1 and ∠3 and ∠2 and ∠4 ∠6 and ∠7 and ∠5 and ∠8

3). In the adjoining figure, p || q. Find the unknown angles.

 125⁰ and ∠e are forming linear pair

  125⁰ + ∠e = 180

∠e = 180 – 125

∠e = 55⁰

∠e and ∠f are vertically opposite angles

∠e = ∠f

But ∠e = 55⁰

∠f = 55⁰

125⁰ and ∠d are pair of corresponding angles

  ∠d = 125⁰

∠d and ∠b are vertically opposite angles

∠d = ∠b

But ∠d = 125⁰

∠b = 125⁰

∠d and ∠c are forming linear pair

  ∠d + ∠c = 180

But ∠d + = 125

∠c = 180 – 125

∠c = 55⁰

∠a and ∠c are vertically opposite angles

∠a = ∠c

But ∠c = 55⁰

∠a = 55⁰

4). Find the value of x in each of the following figures if l || m.

(i)       (ii)

Solution:

(i) let y be the vertically opposite angle of 110⁰

 y = 110⁰                     (vertically opposite angles are congruent)

 l || m and t is transversal

  110⁰ + x⁰ = 180  (interior angles are supplementary)

x⁰ =180 – 110

x⁰ =70⁰

 

(ii) l || m and a is transversal

x = 100⁰                     (corresponding angles are congruent)

 

5). In the given figure, the arms of two angles are parallel. If ∠ABC = 70º, then find

(i) ∠DGC

(ii) ∠DEF

Given: ∠ABC = 70º

AB ||DE and BC || EF     

 Since AB ||DE and BC is transversal

∠ABC and ∠DGC are forming a pair of corresponding angles

∠ABC = ∠DGC

But ∠DGC = 70⁰

∠DGC = 70⁰

Since BC ||EF and DE is transversal

∠DEF and ∠DGC are forming a pair of corresponding angles

∠DEF = ∠DGC

But ∠DGC = 70⁰

∠DEF = 70⁰

6). In the given figures below, decide whether l is parallel to m.

 i). 

  126⁰ + 44⁰ = 170

126⁰ + 44⁰ ≠180

The Sum of interior angles is not equal to 180.

By interior angles test, l is not parallel to m 

 

ii).

let x be the vertically opposite angle of 75⁰

 x = 75⁰                (vertically opposite angles are congruent)

  75⁰ + 75⁰ = 150

75⁰ + 75⁰ ≠180

The Sum of interior angles is not equal to 180

By interior angles test, l is not parallel to m 

iii).

let x be the vertically opposite angle of 57⁰

 x = 57⁰                (vertically opposite angles are congruent)

  57⁰ + 123⁰ = 180

The Sum of interior angles is equal to 180

By interior angles test, l is parallel to m 

iv).

let x be the vertically opposite angle of 72⁰

 x = 72⁰                (vertically opposite angles are congruent)

  72⁰ + 98⁰ = 170

75⁰ + 75⁰ ≠180

The Sum of interior angles is not equal to 180

By interior angles test, l is not parallel to m 

Click here for the solutions of 

Exercise 5.1

Exercise 5.2

Exercise 4.1

Exercise 4.2

Exercise 4.3

Exercise 4.4

Exercise 3.1

Exercise 3.2

Exercise 3.3

Exercise 3.4