The Triangle and Its Properties
Exercise 6.4
1). Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm (ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:
(i) 2 cm, 3 cm, 5 cm
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
the sum of the two sides are
2 + 3 = 5
Third side = 5
the sum of the two sides = third side
therefore, triangle is not possible
(ii) 3 cm, 6 cm, 7 cm
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
the sum of the two sides are
3 + 6 = 9
Third side = 7
the sum of the two sides > the third side
the sum of the two sides are
3 + 7 = 10
Third side = 6
the sum of the two sides > the third side
the sum of the two sides are
7 + 6 = 13
Third side = 3
the sum of the two sides > the third side
therefore, triangle is possible
(iii) 6 cm, 3 cm, 2 cm
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
the sum of the two sides are
2 + 3 = 5
Third side = 6
the sum of the two sides < the third side
therefore, triangle is not possible
2). Take any point O in the interior of a triangle PQR. Is
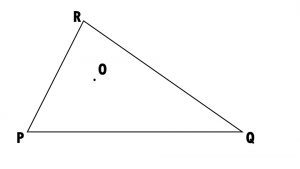
(i) OP + OQ > PQ?
Yes, in DOPQ
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
(ii) OQ + OR > QR?
Yes, in DOQR
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
(iii) OR + OP > RP?
Yes, in DOPR
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
3). AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles DABM and DAMC.)
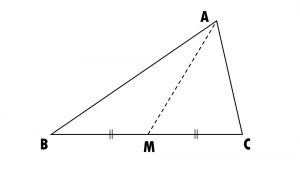
In DAMB
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
AB + BM > AM ……………………(I)
In DAMC
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
AC + CM > AM ……………………(II)
Adding I and II
AB + BM + AC + CM > AM + AM
AB + BM + CM + AC > AM + AM
AB + BC + AC > 2AM
4). ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
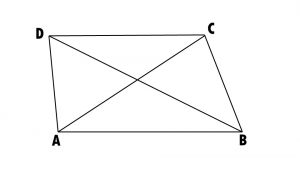
In DABC
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
AB + BC > AC ……………………(I)
In DBCD
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
BC + CD > BD ……………………(II)
In DCDA
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
CD + DA > AC ……………………(III)
In DDAB
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
DA + AB > BD ……………………(IV)
Adding I, II, III and IV
AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD
2AB + 2BC + 2CD + 2DA > 2AC + 2BD
2(AB + BC + CD + DA) > 2(AC + BD)
Dividing both inequalities with 2, we get
AB + BC + CD + DA > AC + BD
5). ABCD is quadrilateral. Is
AB + BC + CD + DA < 2 (AC + BD)?

Let P be the point of intersection of diagonals AC and BD
In DAPB
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
AP + PB > AB ……………………(I)
Similarly In DPCB
PB + PC > BC ……………………(II)
Similarly In DAPD
AP + PD > AD ……………………(III)
Similarly In DCPD
PD + PC > CD ……………………(IV)
Adding I, II, III and IV
AP + PB + PB + PC + AP + PD + PD + PC > AB + BC + AD + CD
2AP + 2PB + 2PC + 2AP > AB + BC + CD + AD
2AP + 2PC + 2PB + 2 > AB + BC + CD + AD
2AC + 2BD > AB + BC + CD + AD
2(AC + BD) > AB + BC + CD + AD
AB + BC + CD + AD < 2(AC + BD)
6). The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Given sides of the triangle are 12 and 15 cm
Therefore, the third side is less than 12 + 15 = 27 cm
The third side cannot be less than the difference of the two sides.
15 – 12 = 3
The third side cannot be less than 3 cm
Therefore, the length of the third side falls between 3 cm and 27 cm.
Click here for the solutions of
![]()
