Be My Multiple, I’ll Be Your Factor
Page 87
a). the steps on which the mouse jumps-
14, 16, 18, 20, 22, 24, 26 and 28.
b). The steps on which the cat jumps-
3, 6, 9, 12, 15, 18, 21, 24, 27 and 30.
c). The steps on which both the cat and the mouse jump-
18 and 24.
d) can the mouse getaway?
Yes, because they both never come together on steps 18 and 24.
Find out
If the cat starts from the 5th step and jump five steps at a time and the mouse starts from the 8th step and jumps four steps at a time, can the mouse getaway?
The steps of the cat are 5, 10, 15, 20, 25 and 30.
The steps of the mouse are 8, 12, 16, 20, 24, 28.
Both the cat and the mouse reach step 20 at the same time, therefore the mouse cannot getaway.
Page 88
Mark with a red dot all the numbers which can be divided by 2.

Mark with a yellow dot on the numbers which can be divided by 3 and a blue dot on the numbers which can be divided by 4.

Which are the boxes which have dots of all three colours?
The boxes containing the numbers 12, 24, 36, 48 and 60 have the dots of all three colours.
What are the letters on top of those boxes?
The letters on the top of those boxes are M, O, U, S and E.
Write those letters below in order.
MOUSE.
Page 89
Which numbers did you replace with ‘Meow’?
3, 6, 9, 12, 15, 18, 21, 24, 27, . . . . . .
Now play this game by changing the number to 4. Now, which numbers did you replace with ‘Meow’?
The numbers replaced with ‘Meow’ are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, . . . . . .
Write any ten multiples of 5.
Ten multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45 and 50.
Page 90
Throw two dice together. What are the numbers that turn up on the faces of the dice? Make a two-digit number using them. If it is a multiple of any of the numbers written next to the circles, you can write it in that circle. Then it is your friend’s turn. The one who can write more numbers in 10 rounds is the winner. I have 3 and 2 on my dice. If I make 23, it is not the multiple of any of the numbers. So I will make 32, which is a multiple of 4, and write in the red circle.
The two digit numbers that can be formed are 11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33 34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65 and 66.
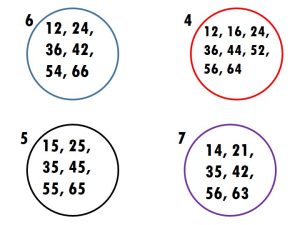
Which is smallest among these common multiples?
15 is the smallest among these common multiples.
Page 91
Think of a number. If it is a multiple of 3 write in the red circle. If it is a multiple of 5 write it in the blue circle.
Where do I write 15? It is a multiple of both 3 and 15

.
Repeat the game using the numbers 2 and 7. Write the common multiples of 2 and 7.
Common multiples of 2 and 7 are 14, 28, 42, 56, 70, . . . . .
Repeat the game by putting the multiples of 4, 6 and 5 in the circles.
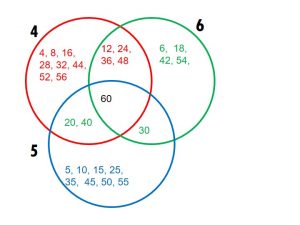
What common multiples of 5 and 6 did you write in the green part?
Common multiples of 5 and 6 are 30, 90, . . . .
What common multiples of 4 and 6 did you write in the orange part?
Common multiples of 4 and 6 are 12, 24, 36, 48, . . . .
In which coloured part did you write the common multiples of 4 and 6 and 5.

What is the smallest common multiple of 4, 5 and 6?
The smallest common multiple of 4, 5 and 6 is 60.
Page 92
Sunita took some tamarind (imli) seeds. She made groups of five with them and found that one seed was leftover. She tried making groups of six and groups of four. Each time one seed was leftover. What is the smallest number of seeds that Sunita had?
The smallest common multiple of 4, 5 and 6 is 60. Therefore, the smallest number of seeds that Sunita had is 60.
How many groups will she have if she makes groups of 1 bangle each?
She will have 60 groups.
Page 93
Ammini is arranging 12 tamarind seeds in the form of different rectangles. Try to make more rectangles like this using 12 tamarind seeds. How many different rectangles can you make?
Three rectangles can be made using 12 tamarind seeds.
If there are 15 tamarind seeds how many rectangles can you make?
Three rectangles can be made using 15 tamarind seeds.
In the grid here, a rectangle made of 20 boxes is drawn. The width of this rectangle is 2 boxes. What is its length?
The length of this rectangle is 10 boxes.
Colour a rectangle made of 20 boxes in some other way.
What is the length and width of the rectangle you coloured?

Length is 5 boxes and width is 4 boxes.
In how many ways can you colour a rectangle of 20 boxes? Colour them all in the grid, and write the length and width of each rectangle you have coloured?
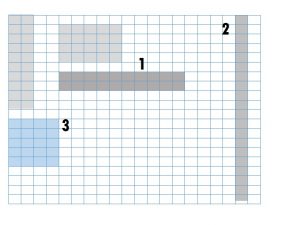
Rectangle 1
Length is 10 boxes and width is 2 boxes.
Rectangle 2
Length is 1 boxes and width is 20 boxes.
Rectangle 3
Length is 4 boxes and width is 5 boxes.
There are 18 bangles on the rod. Meena is trying t group them. She can put them in groups of 2, 3, 6, 9 and 18- without any bangle being left.
How many groups will she have if she makes groups of 1 bangle each?
She will make 18 groups.
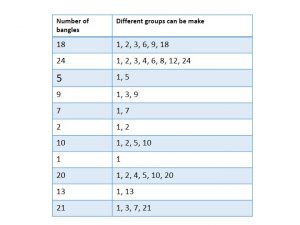
Now complete the table, for different numbers of bangles. For each number see what different groups can be made.
Page 96
What are the factors of 10?
Factors of 10 are 1, 2, 5, and 10.
Can you do this from the chart?
Yes.
What are the factors of 36?
Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.
Find out all the factors of 36 from the multiplication chart.
What is the biggest number for which you can find the factors from this chart?
144.
What can you do for numbers bigger than that?
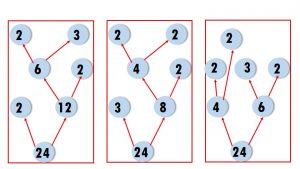
Look at the factor tree. Now can you make another tree like this?
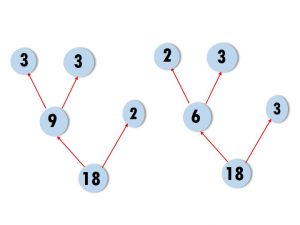
In how many ways can you draw a factor tree for 24? Draw three of them below.
1). There is a garden in Anu’s house. In the middle of the garden, there is a path. They decided to tile the path using tiles of length 2 feet, 3 feet and 5 feet. The mason tiled the first row with 2 feet tiles, the second row with 3 feet tiles and the third row with 5 feet tiles. The mason has not cut any of the tiles. Then what is the shortest length of the path?
The smallest common multiple of 2 feet, 3 feet and 5 feet tile is the shortest lengh.
Multiple of 2 = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30,
32, 34, 36, 38, 40, . . . . . . . . . . .
Multiple of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, . .
Multiple of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, . . . . . .
Common multiple of 2, 3 and 5 = 30, . . . .
The smallest common multiple is 30.
Therefore, the shortest path is 30 feet.
2). Manoj had made a new house. He wants to lay tiles on the floor. The size of the room is 9 feet X 12 feet. In the market there are three kinds of square tiles are available. 1 foot X 1 foot, 2 feet X 2 feet and 3 feet X 3 feet. Which size of tile he should buy for his room, so that he can lay it without cutting?
The size of the room is 9 feet X 12 feet.
Factors of 9 are 1, 3 and 9. 2 is not a factor of 9. Therefore, Manoj has to buy either 1 foot X 1 foot or 3 feet X 3 feet tiles so that he can lay it without cutting.
3). Rani, Geetha and Naseema live near each other. The distance from their house to the road is 90 feet. They decided to tile the path to the road. They all bought tiles of different designs and length. Rani bought the shortest tile, Geetha bought the middle-sized one and Naseema bought the longest one. If they could tile the path without cutting any of the tiles what is the size of the tiles each has bought? Suggest 3 different solutions. Explain how you get this answer.
90 = 1 X 90
2 X 45
3 X 30
5 X 18
6 X 15
9 X 10
So they can buy the tiles of 1 X 1, 2 X 2, 3 X 3, 5 X 5, 6 X 6 etc.
Click here for the solutions of
6). Be My multiple, I’ll Be Your Factor
13). Ways To Multiply and Divide
![]()
